In 2018, I became interested in investing in options (calls and puts), but I wasn’t sure what fair price I should be paying for them. That’s when I discovered the Black-Scholes equation. I built a Python script that:
- Connects with broker APIs to fetch real-time information about available calls and puts
- Retrieves current stock market data
- Web scrapes daily volatility reports
- Creates a database containing all the gathered information and uses the Black-Scholes formula to calculate the theoretical value of options
- Displays those calls being offered below their theoretical Black-Scholes valuation
I made several improvements to this script through the years, making it faster, more reliable, and more accurate.
Let’s Look at the Data
I usually use bullmarketbrokers as my main broker, but due to some problems with their API, I switched to invertironline’s API, which proved to be more reliable. The key point is that the data gathered from both brokers is the same and makes no difference for the analysis.
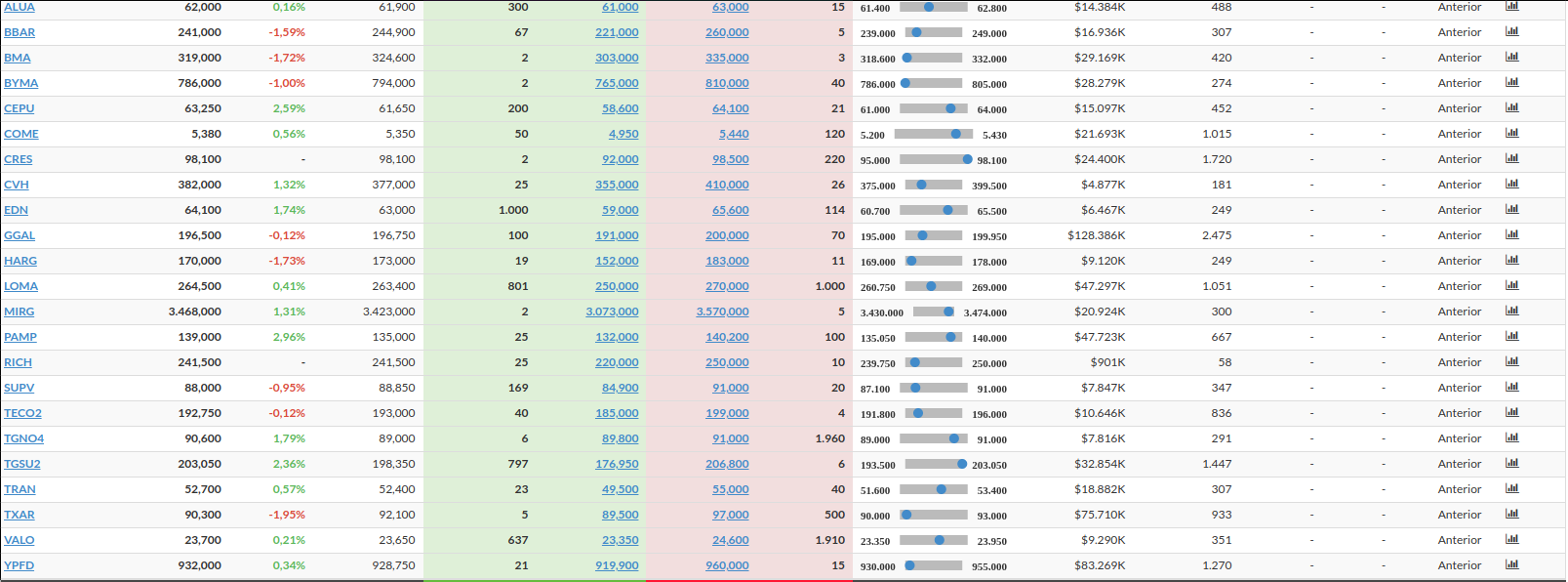
In a normal day we can see a table like this one for the stock market
and like this for puts and calls
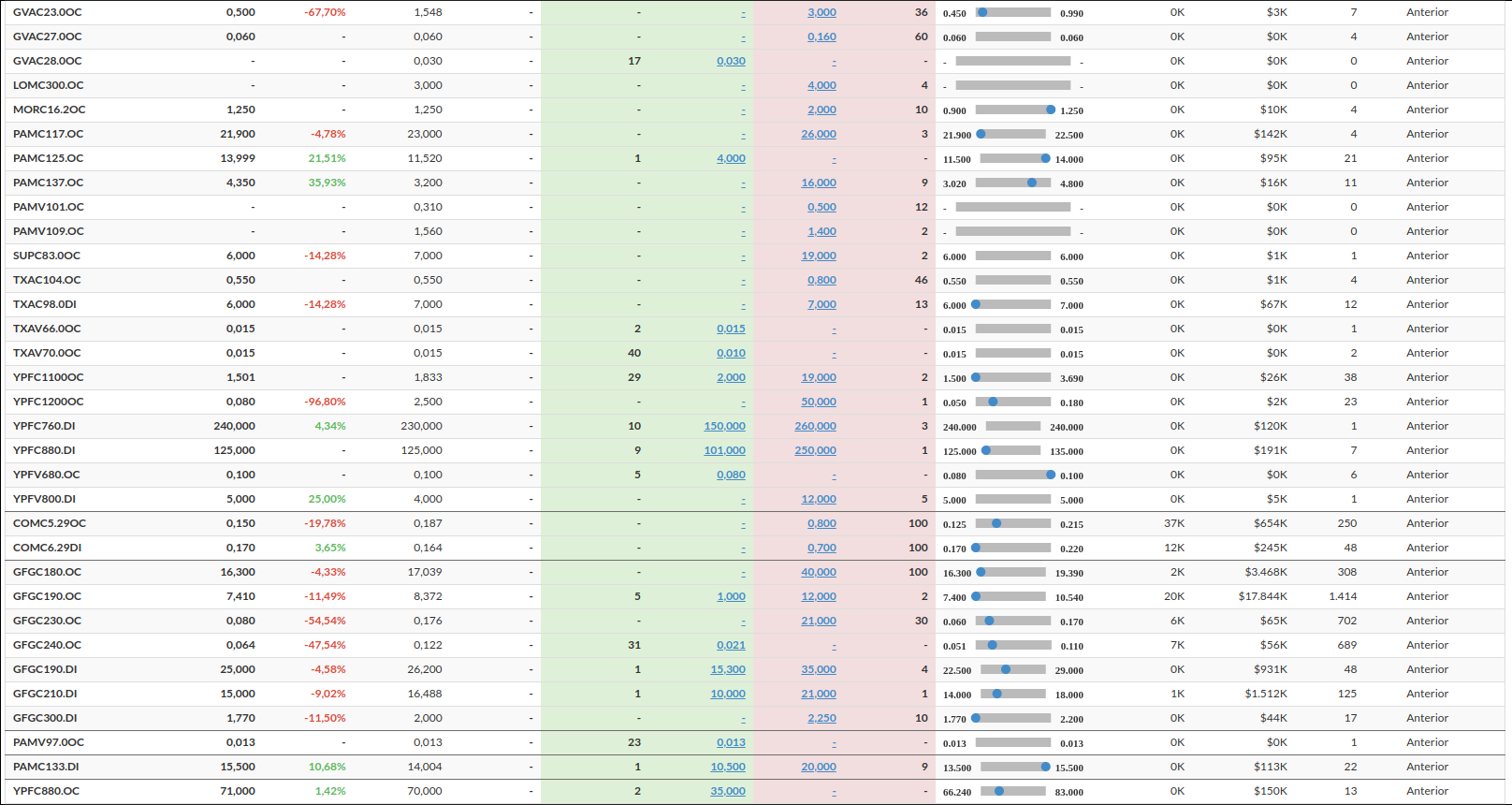
So at the end, we have almost all the data required to perform the calculations using the Black-Scholes formula, with the exception of one critical component: the stock’s volatility.
Volatility
The volatility of each stock is not something you can obtain directly from the broker’s API. Fortunately, there are websites that continuously publish reports about stocks. I included functions that automatically download these reports (in PDF format) and extract the 52-week volatility for all the main stocks, appending this crucial information to the data we already gathered.
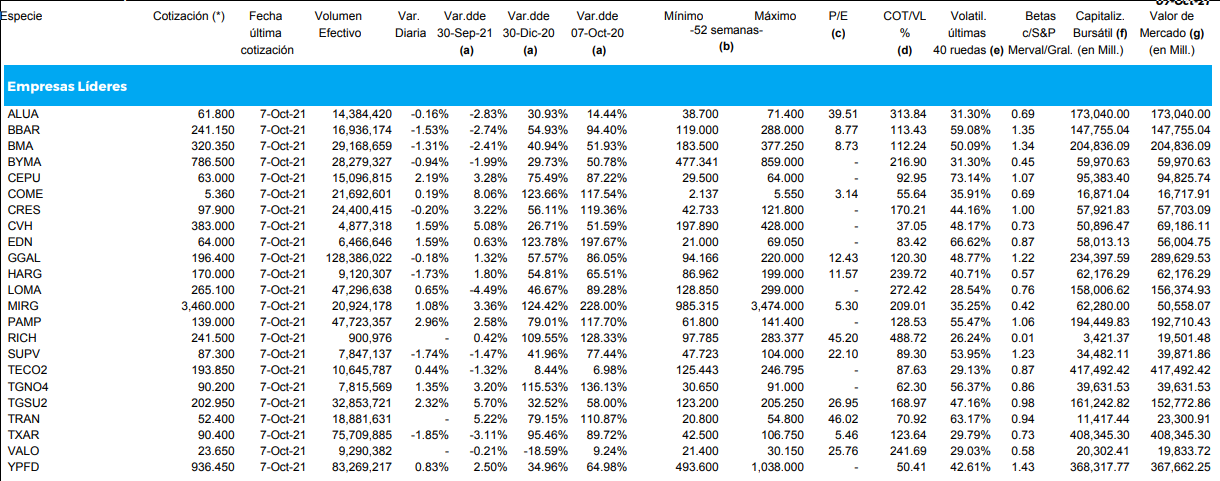
The Scripts
I used pandas, numpy, and math for data analysis, and requests and BeautifulSoup for web scraping.
All the data is gathered and stored locally by simply running Data_opciones.py.
Later, by running Opciones.py, the output looks like this for Calls:
Accion P_A Tipo_opcion Target Vencmt. Opcion_cotizacion Vol Teorico %VT
0 ALUA 67.4 Call 31.0 1.639710e+09 33.70 0.3358 38.45 87.65
1 ALUA 67.4 Call 61.0 1.639710e+09 10.00 0.3358 11.05 90.50
4 ALUA 67.4 Call 69.0 1.639710e+09 5.00 0.3358 5.61 89.13
5 ALUA 67.4 Call 71.0 1.639710e+09 4.00 0.3358 4.59 87.15
6 ALUA 67.4 Call 73.0 1.639710e+09 2.45 0.3358 3.70 66.22
.. ... ... ... ... ... ... ... ... ...
275 YPFD 895.5 Call 880.0 1.639710e+09 92.00 0.4222 108.16 85.06
279 YPFD 895.5 Call 960.0 1.639710e+09 65.00 0.4222 67.10 96.87
282 YPFD 895.5 Call 1000.0 1.639710e+09 45.00 0.4222 51.51 87.36
287 YPFD 895.5 Call 1150.0 1.639710e+09 15.50 0.4222 16.66 93.04
290 YPFD 895.5 Call 1200.0 1.639710e+09 10.00 0.4222 10.96 91.24
All these options are currently priced below their Black-Scholes theoretical value—potentially undervalued opportunities!
Future Enhancements
I’m considering expanding this project to implement multi-leg options strategies (like spreads and straddles) that can offer high-probability profit opportunities in the stock market.