My PhD director developed an elegant algorithm called Wave_clus, written in MATLAB, that clusters signals coming from electrodes in brain patients’ recordings to differentiate the activity from distinct neurons. However, the algorithm can’t automatically decide which “cluster” comes from a neuron versus noise.
Since we already had a large database of clusters, we manually labeled those that were neuron clusters and those that weren’t. The idea of this project was to leverage the fact that neuronal activity can be simulated and characterized by a few parameters of simple dynamical models. Our hypothesis was that these parameter values would allow us to differentiate noise from genuine neuron activity.
We used a novel approach called Sparse Identification of Nonlinear Dynamics (SINDy) with a LASSO regressor to identify the dynamics of our database. Although this was a very interesting approach and I learned a lot, I couldn’t make it work as intended.
The Data
I implemented everything using Jupyter Lab and Python.
In the plot below you can see neuron clusters (Cluster 1) and noisy clusters (Clusters 2, 3) from one of the recordings of neural activity (from the same electrode).
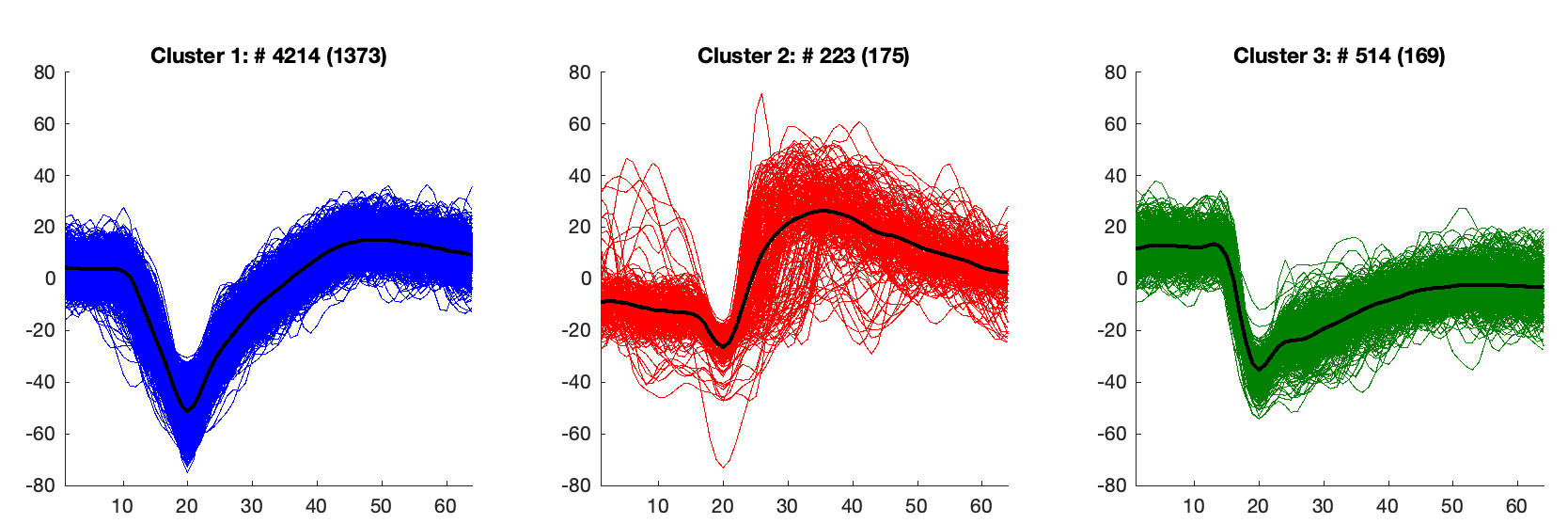
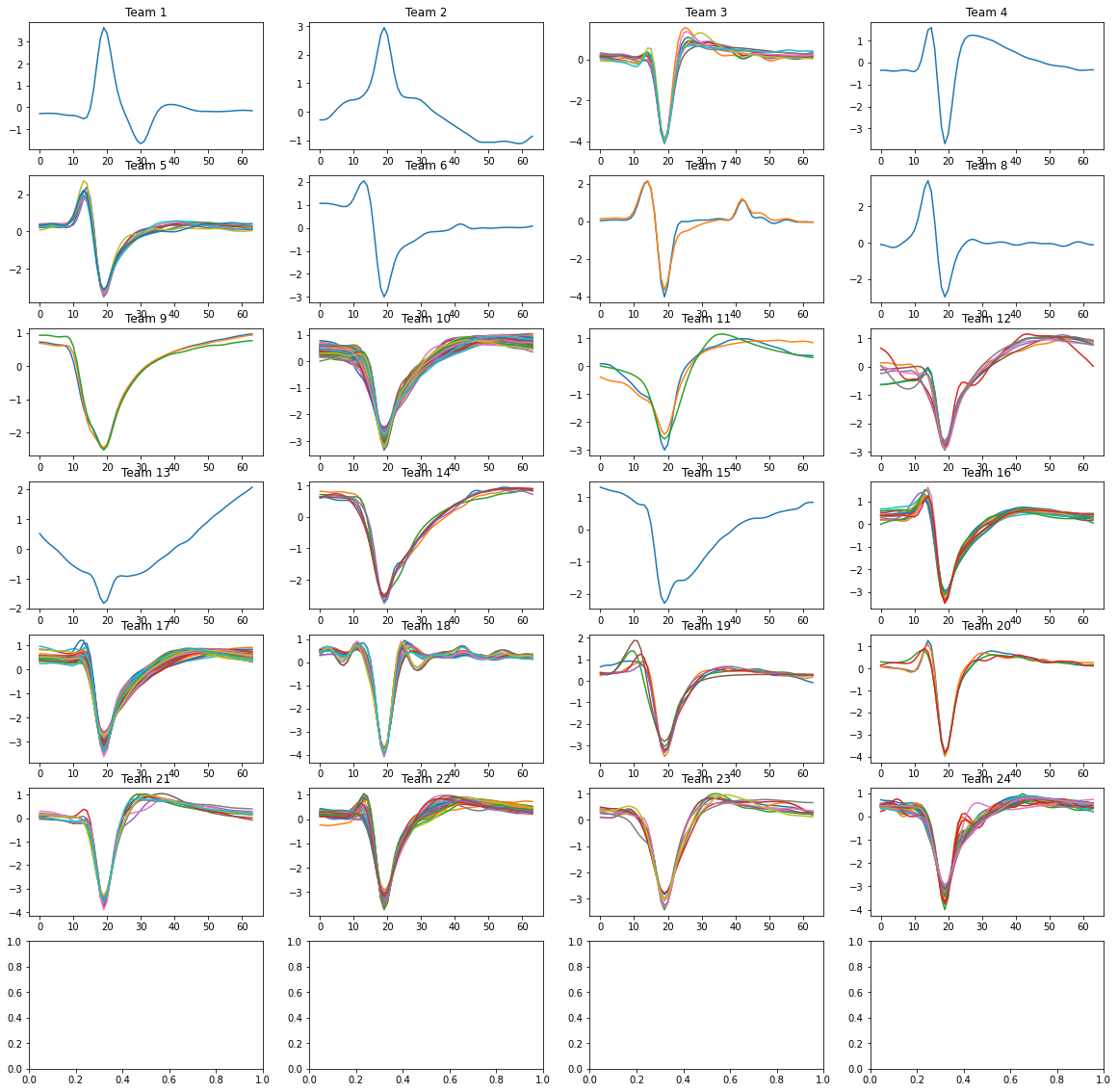
While standard deviation, maximum amplitude, and other features provide information about whether a cluster is noise or not, this project used only the average signal of each cluster. After normalizing and using Hierarchical clustering, I grouped those clusters that shared similarities (neurons only). The results are shown below:
Embeddings
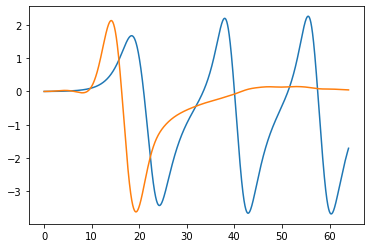
One of the most important concepts for this project was that of embeddings. Since SINDy requires full knowledge of the phase space, an embedding is the way you can reconstruct it via partial observation of the phenomena (in this case, the partial observation was the mean cluster signal). Below is a figure of the approximated phase space recreated from one of the clusters we analyzed.

SINDy Framework
SINDy is a novel framework to discover governing equations underlying a dynamical system simply from data measurements, leveraging advances in sparsity techniques and machine learning. The resulting models are parsimonious, balancing model complexity with descriptive ability while avoiding overfitting.
There are many critical data-driven problems where this approach is valuable: understanding cognition from neural recordings, inferring climate patterns, determining stability of financial markets, predicting and suppressing the spread of disease, and controlling turbulence for greener transportation and energy. With abundant data and elusive laws, data-driven discovery of dynamics will continue to play an important role in these efforts.
Essentially, SINDy is a framework that fits dynamical models to data. The parameter values of that model are what we were looking for. In this case, our model was of the form:
Previous research showed that this model can capture many neuronal dynamics for different parameter values.
Results
While the model parameters were determined for each cluster, the solutions were highly unstable, leading to poor performance on new data. Despite this, I was surprised to see how easy and powerful SINDy is—the results were reasonably close to the true solution in parameter space. I tried interpolating the signals to see if a more stable solution could be obtained, but there were no significant improvements.
Future Work
I’m confident that this approach SHOULD work—spending more time on this project would likely yield better results. Perhaps using a different dynamical model or replacing LASSO with another regularization method could improve solution stability. I really enjoyed working on this project and learned a lot about the intersection of neuroscience and machine learning.